12 Spatial Predicates

In Opensource GIS Applications, there is a common standard to describe various relationships between features. They are referred to as “Spatial predicates” and are defined as follows. Take two geometries, a and b:

• Equals: a and b are equal if
  • their interiors intersect and
  • no part of the interior or boundary of one geometry intersects the exterior of the other
• Disjoint: a and b are disjoint if they have no point in common (they form a set of disconnected geometries)
• Touches: a and b touch if
  • they have at least one point in common but
  • their interiors do not intersect
• Contains: a contains b if
  • no points of b lie in the exterior of a and
  • at least one point of the interior of b lies in the interior of a
• Covers: a covers b if at least one point of b lies in a, and no point of b lies in the exterior of a
• Intersects: a and b intersect if the two geometries have at least one point in common
• Within (inside): a is within b if a lies in the interior of the b
• CoveredBy: a is covered by b if a lies in b
• Crosses: a crosses b if they have some but not all interior points in common.
• Overlaps: a overlaps b
  • if they have some (but not all) points in common and
  • they have the same dimension and
  • the intersection of the interiors of the two geometries has the same dimension as the geometries themselves

12.1 Named predicates

12.1.1 Touches

Lets take the example of a chessboard:

library(sf)
library(dplyr)
library(arc2r)

data("chessboard")


chessplot <- ggplot(chessboard) + geom_sf(aes(fill = colour)) + geom_sf_label(aes(label = i)) + 
    scale_x_continuous(breaks = 1:8 - 0.5, labels = letters[1:8]) + scale_y_continuous(breaks = 1:8 - 
    0.5, labels = 1:8) + scale_fill_manual(values = c(black = "black", white = "white")) + 
    theme_void() + theme(legend.position = "none")

chessplot

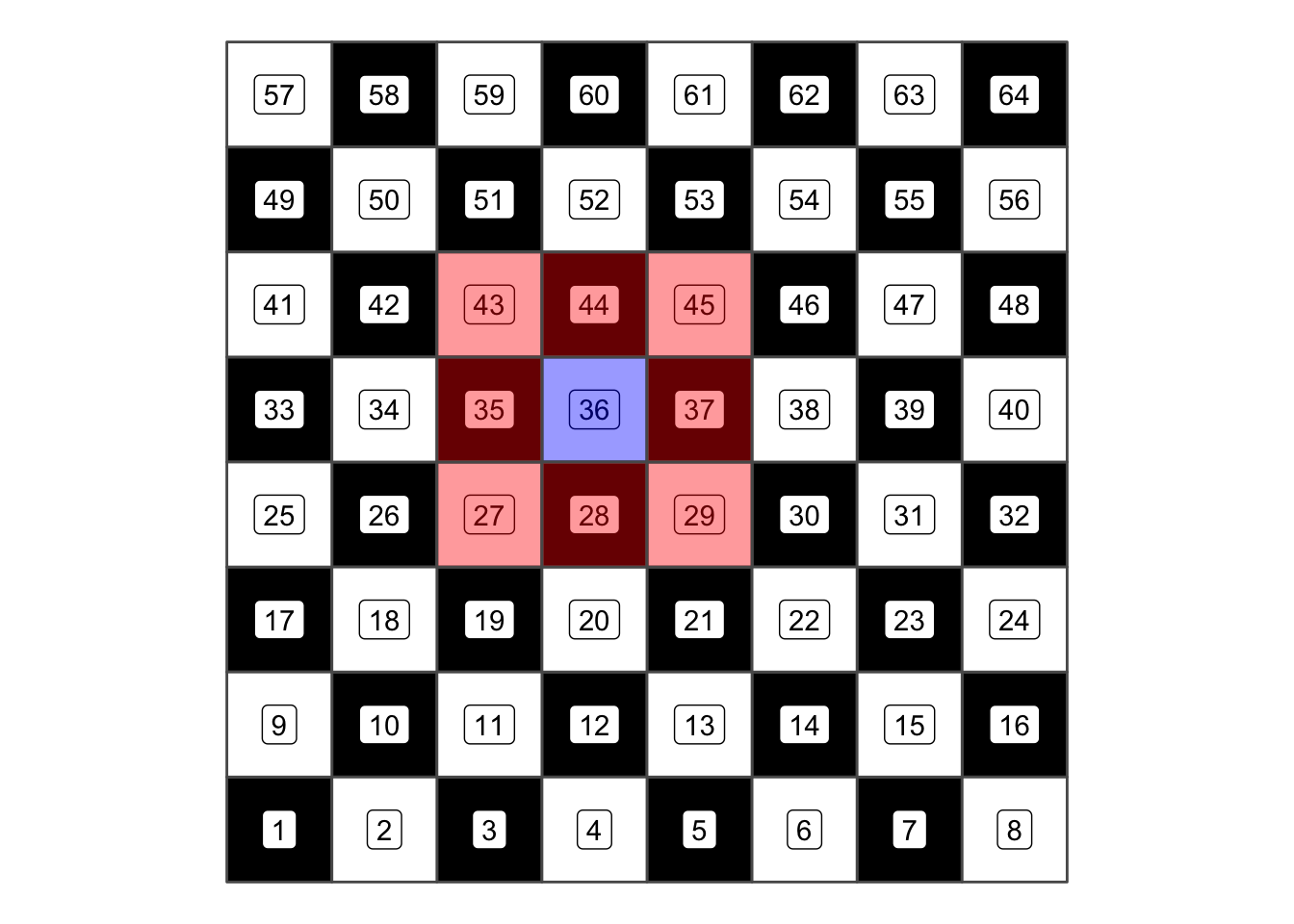
To find out which field touch field number 36, we can write the following line of code:

st_touches(chessboard[36, ], chessboard)

## Sparse geometry binary predicate list of length 1, where the predicate was `touches'
##  1: 27, 28, 29, 35, 37, 43, 44, 45

Visually, these are the following fields:

sel36 <- st_touches(chessboard[36, ], chessboard)[[1]]


chessplot + geom_sf(data = chessboard[36, ], fill = "blue", alpha = 0.4) + geom_sf(data = chessboard[sel36, 
    ], fill = "red", alpha = 0.4)